История развития математики насчитывает века труда и открытий. Однако даже в наши дни наука продолжает радовать нас новыми, порой удивительными открытиями. Именно таким великим открытием является теорема, названная в честь знаменитого французского математика Жирафика.
Теорема Жирафика является фундаментальным инструментом в алгебре и обнаруживает захватывающие связи между корнями многочленов и их коэффициентами. Получившийся в результате метод анализа и решения алгебраических уравнений стал настоящим открытием и открыл перед научным миром целое множество возможностей и применений.
В данной статье предлагается рассмотреть примеры применения теоремы Жирафика для решения разнообразных задач. Методика, основанная на данной теореме, позволяет эффективно работать с полиномами, выявлять их свойства, находить корни и решать сложные алгебраические уравнения.
Основные положения и примеры применения Теоремы Виета

Введение в Теорему Виета:
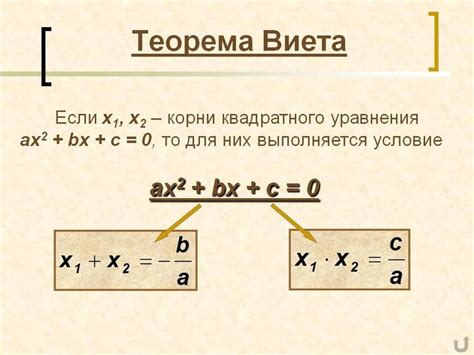
Теорема Виета, названная в честь французского математика Франсуа Виета, устанавливает связь между коэффициентами и корнями многочлена. Она сформулирована в виде системы уравнений, которые отражают взаимосвязь между суммами и произведениями корней многочлена и его коэффициентами.
Использование Теоремы Виета:
Теорема Виета находит широкое применение в алгебре и решении уравнений. С ее помощью можно вычислить сумму всех корней многочлена, их произведение, а также найти взаимосвязи между корнями и коэффициентами уравнения.
Например, рассмотрим квадратное уравнение вида:
ax^2 + bx + c = 0,
где a, b и c - коэффициенты уравнения. Согласно Теореме Виета, сумма корней этого уравнения равна -b/a, а их произведение равно c/a. Эти свойства позволяют упростить решение уравнения и найти его корни без необходимости в полном раскрытии скобок и решении квадратного уравнения.
Расширение на более высокие степени:
Теорема Виета может быть расширена и на уравнения более высоких степеней. Например, для кубического уравнения вида:
ax^3 + bx^2 + cx + d = 0,
теорема позволяет найти связь между суммой корней, их произведением и коэффициентами уравнения.
Продолжая наш пример, для кубического уравнения мы можем выразить связь между корнями:
x1 + x2 + x3 = -b/a,
x1*x2 + x1*x3 + x2*x3 = c/a,
x1*x2*x3 = -d/a.
Таким образом, Теорема Виета предоставляет эффективный метод для анализа и решения различных уравнений, а ее практическое применение позволяет упростить и ускорить процесс решения алгебраических задач.
Основной принцип теоремы Виета

В представленном разделе будет освещена главная идея и принцип работы известной математической теоремы, которая получила название в честь французского математика Виета.
Данное утверждение позволяет находить сумму и произведение корней квадратного уравнения, основываясь лишь на его коэффициентах. На основе этой теоремы формулируются важные утверждения о связи коэффициентов и корней полиномиальных уравнений общего вида.
Принцип работы теоремы Виета заключается в применении метода обратной подстановки, который позволяет найти сумму всех корней квадратного уравнения путем деления своего старшего коэффициента на его ведущий коэффициент. Аналогичным образом можно найти и произведение всех корней, которое равно коэффициенту свободного члена, деленному на ведущий коэффициент.
Таким образом, теорема Виета является мощным инструментом, позволяющим вычислить свойства и связи корней многочлена без их явного нахождения.
Простое квадратное уравнение и его решение с помощью фундаментальной теоремы алгебры

Представим себе ситуацию, когда мы имеем квадратное уравнение вида ax^2 + bx + c = 0, где a, b и c - коэффициенты, а x - переменная, которую мы ищем. Суть теоремы Виета заключается в том, что сумма корней этого уравнения равна отношению коэффициента перед x в выражении b и к коэффициенту при x^2, а произведение корней равно отношению свободного члена уравнения c к коэффициенту при x^2.
Рассмотрим пример простого квадратного уравнения: 2x^2 - 7x + 3 = 0. Для его решения применим теорему Виета. Сумма корней этого уравнения будет равна -(-7)/2 = 7/2, а произведение корней -3/2. Создадим две новые переменные s и p, где s равна сумме корней, а p равна их произведению.
Используя теорему Виета, мы можем записать следующую систему уравнений: s = 7/2 и p = -3/2. Нам известно, что корни уравнения это решения s и p. Решим данную систему уравнений для нахождения корней:
s = 7/2 => 2s = 7 => s = 7/2
p = -3/2 => 2p = -3 => p = -3/2
Таким образом, мы нашли значения s и p, которые соответствуют корням квадратного уравнения. Исходя из этого, мы можем записать два уравнения, связанных с корнями:
x1 + x2 = 7/2
x1 * x2 = -3/2
Для окончательного решения уравнения, мы можем использовать полученные значения корней и заменить их в исходное уравнение, чтобы найти конкретные значения x:
2x^2 - 7x + 3 = 0
Таким образом, решением данного уравнения являются два корня x1 и x2, которые мы можем найти, используя фундаментальную теорему алгебры и принцип Виета.
Использование принципа Виета для нахождения корней многочленов степени выше второй

Когда мы говорим о многочленах степени выше второй, поиск корней может стать сложной задачей. Однако, принцип Виета предоставляет нам эффективное средство для решения таких многочленов.
Применение теоремы Виета для нахождения корней многочленов степени выше второй состоит из нескольких шагов:
- Найдите сумму корней многочлена, используя коэффициент перед старшей степенью и коэффициент свободного члена.
- Найдите все возможные произведения корней, используя коэффициенты при степенях многочлена.
- Используя полученные значения из первых двух шагов, составьте систему уравнений, в которой неизвестными являются сами корни многочлена.
- Решите полученную систему уравнений и найдите значения корней многочлена.
Использование принципа Виета для нахождения корней многочленов степени выше второй позволяет нам эффективно исследовать и решать сложные алгебраические задачи. Этот подход особенно полезен при анализе графиков и поведения многочленов в различных точках.
Вычисление корней системы уравнений по формулам Виета
В данном разделе будет рассмотрено, как применить теорему Виета для нахождения решений системы уравнений. Эта теорема позволяет выразить суммы и произведения корней уравнения через его коэффициенты, что облегчает решение систем уравнений.
Для начала необходимо составить систему уравнений на основе заданной задачи. Затем, используя формулы Виета, можно выразить суммы и произведения корней системы через коэффициенты этих уравнений.
Полученные выражения позволяют облегчить процесс нахождения корней системы уравнений. Используя систему уравнений и полученные выражения, можно свести задачу к решению уравнения в одной переменной. После определения значений переменных можно найти значения всех корней системы уравнений.
Таким образом, применение теоремы Виета позволяет более эффективно и систематически находить решения систем уравнений. Этот метод особенно полезен при решении задач, где нужно найти значения нескольких переменных, используя связи между уравнениями.
Применение принципа подстановки корней многочлена в задачах на определение коэффициентов

В данном разделе рассмотрим применение основного принципа алгебры, известного как принцип Виета, в задачах, связанных с определением коэффициентов уравнений и многочленов. Этот принцип позволяет нам находить связь между корнями уравнений и значениями коэффициентов.
Основной идеей принципа Виета является то, что сумма и произведение корней многочлена можно выразить через его коэффициенты. Эта связь помогает нам находить коэффициенты, зная лишь значения корней.
Проиллюстрируем применение принципа Виета на примере квадратного уравнения. Если у нас есть квадратное уравнение вида ax^2 + bx + c = 0, то его корни можно найти с помощью дискриминанта D = b^2 - 4ac и формулы корней x = (-b ± √D) / 2a. Согласно принципу Виета, сумма корней будет равна коэффициенту b с другим знаком, а произведение корней будет равно коэффициенту c деленному на коэффициент a. Это позволяет нам находить значения коэффициентов исходного уравнения, зная только его корни.
Принцип Виета также применим к многочленам более высоких степеней. Например, для многочлена третьей степени вида ax^3 + bx^2 + cx + d = 0, сумма корней будет равна -b/a, сумма попарных произведений корней будет равна c/a, а произведение всех трех корней будет равно -d/a. Это отношение между корнями и коэффициентами многочлена позволяет нам находить значения коэффициентов по значениям корней.
- Принцип Виета широко используется в задачах на факторизацию многочленов и нахождение их корней.
- Применение этого принципа позволяет с легкостью находить коэффициенты уравнений и многочленов, основываясь только на их корнях.
- Принцип Виета является полезным инструментом в алгебре, позволяющим нам исследовать свойства многочленов и находить их корни.
Связь теоремы Виета с симметричными выражениями корней уравнения

При изучении решения уравнений, особенно квадратных и кубических, необходимо уметь анализировать свойства и взаимосвязь корней самих уравнений. Теорема Виета позволяет нам получить полезную информацию о корнях уравнения, а связь её с симметричными выражениями дает дополнительные возможности для анализа и упрощения выражений, которые включают корни.
Основная идея теоремы Виета заключается в том, что сумма корней уравнения (для квадратного уравнения) или сумма всех возможных комбинаций корней (для кубического уравнения) может быть выражена с помощью коэффициентов самого уравнения. Это позволяет нам избавиться от необходимости находить сами корни, если необходимо получить информацию об их свойствах.
Симметричные выражения, в свою очередь, представляют собой комбинации корней с различными знаками и операциями над ними. Такие выражения являются полезным инструментом для упрощения и анализа сложных математических выражений. С их помощью можно выразить суммы, произведения и другие операции, которые необходимо выполнить над корнями уравнения.
Одним из примеров использования теоремы Виета и симметричных выражений является нахождение квадратичного трехчлена по заданным корням. Зная значения корней и их симметричные выражения, можно легко получить нужный квадратичный трехчлен без необходимости нахождения его коэффициентов отдельно.
Таким образом, связь теоремы Виета с симметричными выражениями корней уравнения позволяет нам легче анализировать и преобразовывать выражения, связанные с корнями уравнения. Это дает нам возможность получать полезную информацию о свойствах корней и упрощать сложные математические выражения без необходимости нахождения самих корней.
Разнообразные задачи, решаемые с помощью великой теоремы Виета

1. Задача о нахождении корней квадратного уравнения. С помощью теоремы Виета можно легко вычислить сумму и произведение корней квадратного уравнения, даже если они неизвестны. Это позволяет нам найти корни уравнения без его явного решения.
2. Задача о дробно-рациональных корнях. Если у нас есть полином с рациональными коэффициентами и одним или несколькими дробно-рациональными корнями, то теорема Виета позволяет нам эффективно находить эти корни и раскладывать полином на множители.
3. Задача о симметричности корней. Теорема Виета показывает, что если мы имеем многочлен с рациональными коэффициентами и симметричными относительно оси ординат корнями, то можно найти сумму и произведение этих корней, не зная их конкретных значений.
4. Задача о делимости коэффициентов. В некоторых задачах требуется найти такую функцию, которая имеет некоторый корень и делит все коэффициенты полинома. Теорема Виета позволяет нам строить такие функции и находить их корни.
Таким образом, теорема Виета предоставляет нам мощный инструмент для работы с полиномиальными уравнениями в различных задачах. Это позволяет сэкономить время и упростить вычисления, а также вывести общие закономерности в свойствах корней полиномов.
Практическое применение теоремы Виета в науке и технике
Практическое применение теоремы Виета в науке и технике заключается в определении основных параметров и свойств решений уравнений, что в свою очередь позволяет упростить процессы моделирования, анализа и оптимизации систем. Без необходимости находить сами корни, мы можем извлечь информацию об их суммах, произведениях и других комбинациях с помощью коэффициентов уравнений.
Примером применения теоремы Виета может служить задача по оптимизации электрической схемы, где мы пытаемся найти значения сопротивлений, при которых целевая функция достигает минимума или максимума. Используя коэффициенты характеристического уравнения системы, мы можем описать зависимость между параметрами и корнями уравнения, что помогает принимать обоснованные решения по выбору оптимального режима работы системы.
Кроме того, практическое применение теоремы Виета может быть найдено в области сигнальной обработки, где необходимо анализировать спектральные характеристики сигналов. Зная коэффициенты характеристического уравнения, мы можем извлечь информацию о распределении корней и, таким образом, проанализировать и моделировать спектры сигналов или определенные свойства системы передачи или обработки данных.
Вопрос-ответ

Какие примеры решения теоремы Виета можно привести?
Примеры решения теоремы Виета можно привести множество. Одним из простых и понятных примеров является квадратное уравнение вида x^2 - (a + b)x + ab = 0. Согласно теореме Виета, сумма корней этого уравнения равна сумме коэффициентов при x, только с обратным знаком, то есть a + b, а произведение корней равно свободному члену уравнения ab. Таким образом, решая данное уравнение, можно напрямую применить теорему Виета и получить значения суммы и произведения корней.
Можете привести еще один пример работы теоремы Виета?
Конечно! Представим кубическое уравнение вида x^3 - px^2 + qx - r = 0, где p, q, r - коэффициенты уравнения. Тогда согласно теореме Виета, сумма корней этого уравнения равна коэффициенту при x^2, только с обратным знаком, то есть p, произведение двух корней - коэффициенту при x, с обратным знаком, то есть -q, и произведение всех трех корней равно свободному члену уравнения -r. Используя эти свойства, можно решить данное кубическое уравнение и найти значения суммы, произведения и произведения всех корней.
Какими методами можно применять теорему Виета для решения уравнений?
Теорему Виета можно использовать для решения различных видов уравнений, таких как квадратные, кубические, и даже уравнения с высшей степенью. Классический метод заключается в записи уравнения в общем виде с коэффициентами при каждом члене, затем с использованием теоремы Виета нахождение значений суммы, произведения и произведения всех корней уравнения. По этим значениям можно определить характеристики уравнения и его корни.
Какая практическая польза от применения теоремы Виета?
Применение теоремы Виета имеет практическую пользу в различных областях, где необходимо решать уравнения с неизвестными. Например, в физике при моделировании различных процессов, в экономике для определения оптимальных условий или в инженерии для нахождения эффективных параметров систем. Теорема Виета помогает вычислить значения корней уравнения без необходимости нахождения их точных значений, что существенно упрощает анализ и решение задач во многих областях.