Когда речь заходит о конструировании фигур в аксонометрической проекции, мы обычно проводим линии и строим геометрические формы в соответствии с классическими правилами. Однако этот подход определяет ограниченный объем решений и не всегда позволяет нам охватить все возможности, которые предоставляет аксонометрия. В связи с этим предлагается альтернативный подход – использование циркуля для построения эллипсов в аксонометрической проекции.
Циркуль, как инструмент, позволяет создавать множество кривых, сфер и эллипсов, а также пространственные фигуры в проекции. Использование циркуля в аксонометрии расширяет возможности проекционных методов, открывая новые горизонты для исследования и применения.
В данной статье мы рассмотрим принцип построения эллипса в аксонометрической проекции с использованием циркуля. Прежде всего, мы ознакомимся с основными принципами работы циркуля и его специфическим применением в аксонометрии. Затем мы рассмотрим конкретные шаги, необходимые для построения эллипса, и приведем примеры его применения на практике. Этот метод будет полезен для всех, кто интересуется аксонометрией и хочет получить более широкий функционал при создании аксонометрических изображений.
Особенности аксонометрии и ее понятие в графическом проектировании
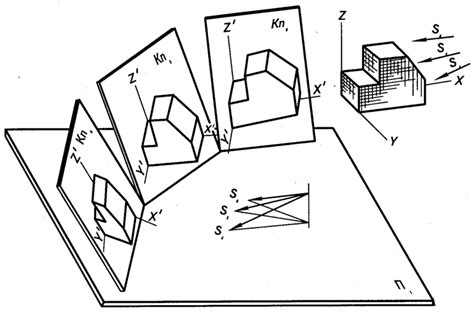
Ключевой особенностью аксонометрии является сохранение всех трех измерений объекта - длины, ширины и высоты. В аксонометрии объекты изображаются так, как они выглядят наблюдателю под определенным углом, не искажая пропорции. Это позволяет визуализировать объекты в полном объеме, что делает аксонометрию важным инструментом в архитектуре, инженерии и дизайне.
- Аксонометрические проекции обладают простой и интуитивно понятной системой координат, что позволяет удобно работать с трехмерными моделями и проектировать объекты в пространстве.
- Аксонометрия позволяет создавать объемные изображения, которые легко воспринимаются человеческим взглядом и передают наглядное представление о трехмерной форме объекта.
- Однако аксонометрия имеет свои ограничения - невозможность точно передать перспективу и расстояния между объектами. В аксонометрических проекциях все линии параллельны осям координат, в то время как в реальности они могут отклоняться и сходиться.
Понимание и учет особенностей аксонометрии является важным аспектом при создании трехмерных моделей и визуализации объектов. Раздел дает общее представление об аксонометрии и ее значении в графическом проектировании, подчеркивая какие возможности и ограничения сопутствуют данному методу отображения трехмерных форм.
Сущность и характеристики эллипса в аксонометрии
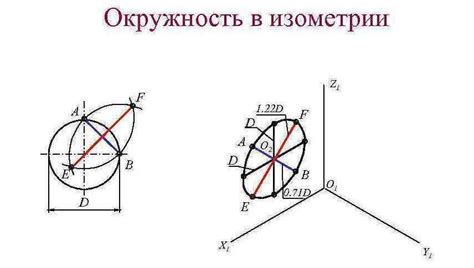
Одной из основных характеристик эллипса является его фокусное свойство, то есть наличие двух точек - фокусов - каждая из которых является фокусным множеством всех точек этой кривой. Также эллипс имеет большую и малую полуоси, которые определяют его размер и форму. Величина большой полуоси называется мажорной осью эллипса, а величина малой полуоси - минорной осью. В отличие от окружности, у которой все полуоси равны, у эллипса они могут быть разными, что придает ему более разнообразные формы.
Кроме того, эллипс обладает симметрией, которая является важным аспектом его аксонометрического изображения. Эта симметрия позволяет получить более точное представление о форме и расстояниях внутри эллипса. Для построения эллипса с использованием циркуля в аксонометрии необходимо учитывать его характеристики и пропорции для достижения точности и соответствия оригинальному объекту.
Построение эллипса в аксонометрии с использованием циркуля: основные концепции и методы
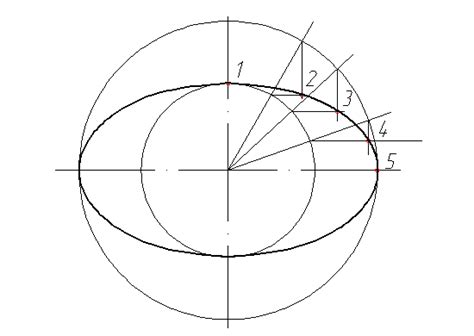
В данном разделе мы рассмотрим методы построения эллипса в аксонометрии, используя циркульные действия. Процесс построения эллипса в трехмерном пространстве требует применения специфических приемов, которые позволяют учесть особенности аксонометрической проекции и достичь максимальной точности и реалистичности изображения без использования сложных геометрических формул.
Применение базовых инструментов
Для построения эллипса в аксонометрии с помощью циркуля мы используем базовые инструменты, такие как циркуль, которые дают возможность проводить окружности, и карандаш для отображения линий и контуров.
Определение центра и ориентация эллипса
В начале процесса необходимо определить центр эллипса, который будет основной точкой отсчета для построения. Далее, использование циркуля позволяет нам установить ориентацию эллипса относительно его центра и аксонометрической плоскости. Это позволяет создать правильную форму и угловую перспективу для эллипса.
Сегментация и отсечение
Далее, мы приступаем к построению сегментов эллипса с использованием циркуля. Разделение эллипса на сегменты позволяет нам более точно определить его форму и размеры. После этого процесса мы можем провести отсечение некоторых сегментов, чтобы достичь требуемой степени детализации изображения и создать эффект объемного представления.
Финальная доработка и декорирование
После построения основной формы эллипса с использованием циркуля, мы можем перейти к финальной доработке и декорированию изображения. Это может включать в себя добавление теней, текстур, цветовых оттенков и других деталей, чтобы придать изображению более реалистичный и привлекательный вид.
Таким образом, построение эллипса в аксонометрии с использованием циркуля требует применения определенных методов и приемов, которые позволяют достичь максимальной точности и реалистичности изображения. Использование циркуля позволяет более удобно и эффективно строить эллипсы, а применение различных приемов и инструментов дает возможность добиться желаемых эффектов и результатов.
Примеры сферического рисования эллипсов в трехмерной графике с использованием изометрии и линейки
Рассмотрим различные способы представления эллипсов - от классической окружности до плоского эллипса, наклонного относительно плоскости изометрической проекции. Каждый пример сопровождается пошаговым описанием действий, необходимых для построения эллипса с помощью линейки и визуальным представлением результатов.
Важные особенности и нюансы сферического рисования в аксонометрии также будут рассмотрены в данных примерах. Особое внимание будет уделено правильному использованию линейки и выравниванию эллипсов для достижения качественных и эстетически приятных результатов.
Вопрос-ответ

Можно ли построить эллипс в аксонометрии без использования циркуля?
Нет, для построения эллипса в аксонометрии требуется использование циркуля.
Каким образом циркуль помогает в построении эллипса в аксонометрии?
Циркуль позволяет очертить дуги, которые задают форму эллипса, позволяя построить его максимально точно.
Какие данные необходимо знать для построения эллипса в аксонометрии?
Для построения эллипса в аксонометрии необходимы значения полуосей эллипса и его центра.
Какие преимущества имеет построение эллипса в аксонометрии с использованием циркуля?
Построение эллипса с помощью циркуля позволяет получить более точный результат, исключая возможные ошибки при отрисовке кривых.
Какая техника использования циркуля при построении эллипса в аксонометрии наиболее эффективна?
Наиболее эффективной техникой использования циркуля при построении эллипса в аксонометрии будет сочетание поворотов и параллельных перемещений.
Каким образом можно построить эллипс в аксонометрии?
Эллипс в аксонометрии можно построить с помощью циркуля. Для этого нужно задать две оси эллипса, а затем окружностью с центром в одном из фокусов эллипса и радиусом, равным полуоси, отметить точки на окружности и провести вспомогательные прямые. Затем, проведя перпендикулярные прямые из точек пересечения вспомогательных прямых с другой осью, можно получить точки эллипса.